amnero.blogg.se

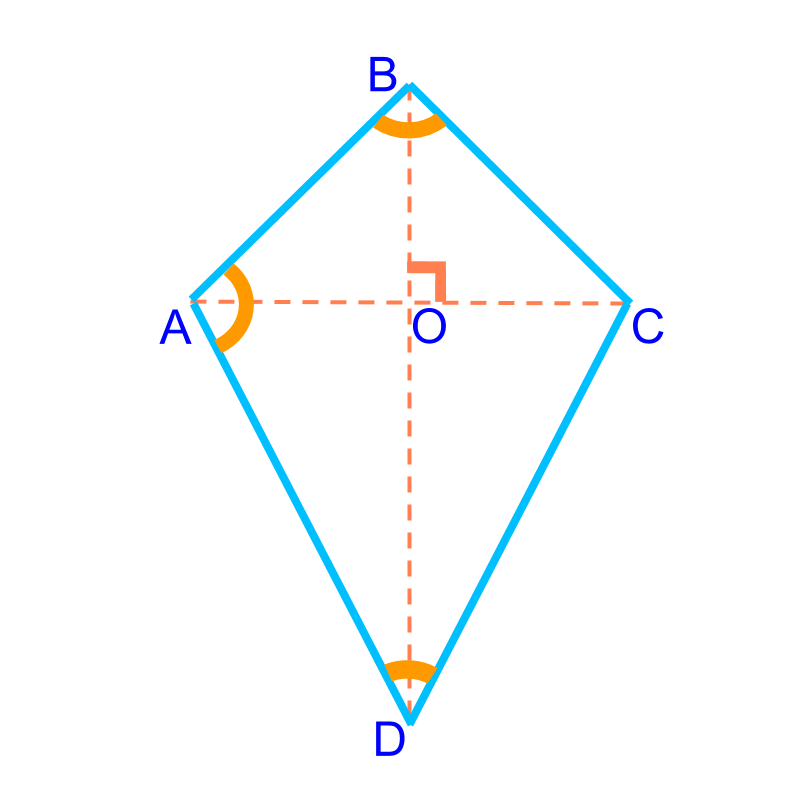
One of the diagonals in a kite bisects its non-congruent angles. Diagonal AC is the perpendicular bisector of diagonal BD.ĭiagonals that bisect the angles of a kite

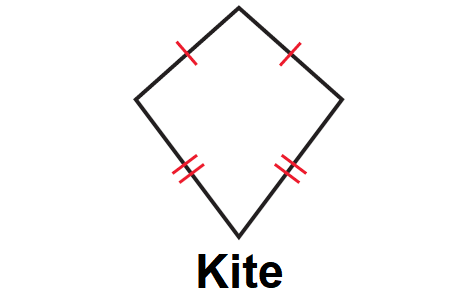
A quadrilateral that has an axis of symmetry must be either a kite. Therefore, diagonals AC and BD are perpendicular. Equivalently, a kite is a quadrilateral with an axis of symmetry along one of its diagonals. Based on this, we know that line segment from A and C to the midpoint of BD is the heights of △ABD and △CBD. Therefore, △ABD and △CBD are isosceles triangles that share a base, BD. Diagonals of a kiteĭiagonals are perpendicular to each other:įor kite ABCD shown above, BA ≅ DA and BC ≅ DC. Sides AB and BC and sides CD and DA are adjacent non-congruent sides for kite ABCD above, so ∠B≅∠D. The angles formed by the adjacent, non-congruent sides of the kite are congruent. Unlike a parallelogram the congruent pairs of sides are not opposite of each other.įor kite ABCD above, congruent sides BC and CD are adjacent to each other as are congruent sides AB and AD. Like a parallelogram, a kite has two pairs of congruent sides. Sides and angles of a kite Sides of a kite

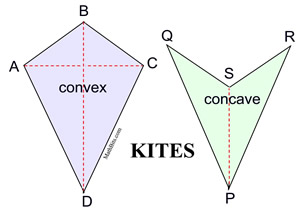
You may think of the kite that can fly, like the one below, when you think of the shape of a kite. These equal sides share a vertex, or "corner." By definition, a kite shape may be either convex or concave, but it is often shown only in its convex form. In mathematics, a kite shape is a quadrilateral with two pairs of sides that are of equal length.